PyTorch Fundamentals: Your First Steps into Hands-on Deep Learning

Covering tensor initialization, operations, indexing, and reshaping.

Mar 30, 2025

Today, I want to talk about the fundamentals of the PyTorch Deep Learning Framework, and I’ll be sharing some code examples along the way.

Why? Many readers of AwesomeNeuron are beginners, and before diving into advanced topics like Transformers, Attention Mechanisms, and LLMs, it's important to build a solid foundation in PyTorch. Mastering the basics will make implementation much easier.

PyTorch is one of the most loved deep learning frameworks among working professionals and researchers, widely used across the industry. While its vast range of capabilities can feel overwhelming at first, building a strong foundation in the fundamentals will make it much easier to get started.

Prerequisite: Basic understanding of Python is MUST!

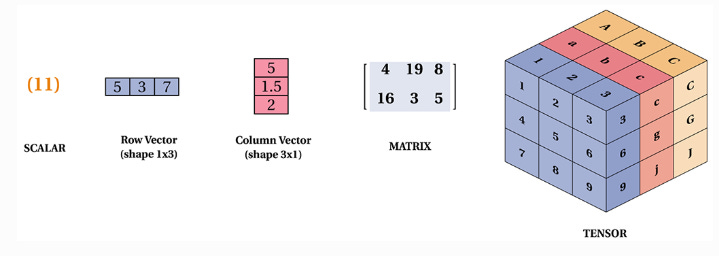
What are Tensors?

Tensor holds a multi-dimensional array of elements of a single data type which is very similar with numpy’s ndarray. When the dimension is zero, it can be called a scalar. When the dimension is 1, it can be called a vector. When the dimension is 2, it can be called a matrix.

0-dimensional tensor: A single number (scalar).
1-dimensional tensor: A list of numbers (vector).
2-dimensional tensor: A table of numbers (matrix).

When the dimension is greater than 2, it is usually called a tensor.

Tensor Initialization

This code creates a 2×3 PyTorch tensor with float32 data type, assigns it to a specified device (CPU or GPU), and enables gradient tracking for backpropagation.

# Initialize a 2x3 tensor with requires_grad enabled
my_tensor = torch.tensor([[1, 2, 3], [4, 5, 6]], dtype=torch.float32, device=device, requires_grad=True)

Common Tensor Initialization Methods

Empty Tensor: Creates an uninitialized 3×3 tensor (random values).
Zeros Tensor: Creates a 3×3 tensor filled with zeros.
Random Tensor: Generates a 3×3 tensor with random values between 0 and 1.
Ones Tensor: Creates a 3×3 tensor filled with ones.
Identity Matrix: Generates a 4×4 identity matrix (diagonal of ones).
Arange Tensor: Creates a 1D tensor with values from 0 to 4 (step of 1).
Linspace Tensor: Generates 5 evenly spaced values between 0.1 and 1.
Normal Distributed Tensor: Fills a tensor with values from a normal (Gaussian) distribution with mean 0 and std 1.
Uniform Distributed Tensor: Fills a tensor with values from a uniform distribution between 0 and 1.
Diagonal Tensor: Creates a 4×4 diagonal tensor with ones along the diagonal and zeros elsewhere.

# Create an empty tensor of size 3x3
x = torch.empty(3, 3)
print("Empty Tensor:\n", x)

# Create a tensor filled with zeros
x = torch.zeros(3, 3)
print("Zeros Tensor:\n", x)

# Create a tensor with random values
x = torch.rand(3, 3)
print("Random Tensor:\n", x)

# Create a tensor filled with ones
x = torch.ones(3, 3)
print("Ones Tensor:\n", x)

# Create an identity matrix
x = torch.eye(4, 4)
print("Identity Matrix:\n", x)

# Create a tensor using arange
x = torch.arange(5)
print("Arange Tensor:\n", x)

# Create a tensor using linspace
x = torch.linspace(0.1, 1, 5)
print("Linspace Tensor:\n", x)

# Create a tensor with values drawn from a normal distribution
x = torch.empty(1, 5).normal_(mean=0, std=1)
print("Normal Distributed Tensor:\n", x)

# Create a tensor with values drawn from a uniform distribution
x = torch.empty(1, 5).uniform_(0, 1)
print("Uniform Distributed Tensor:\n", x)

# Create a diagonal tensor from a tensor of ones
x = torch.diag(torch.ones(4))
print("Diagonal Tensor:\n", x)

Tensor Type Conversion

Creates a tensor with values [0, 1, 2, 3] and demonstrates type conversion to boolean, int16, int64, float16, float32, and float64.

# Create a tensor and convert its type
tensor = torch.arange(4)
print("Boolean Tensor:", tensor.bool())   # Convert to boolean
print("Short Tensor (int16):", tensor.short())   # Convert to int16
print("Long Tensor (int64):", tensor.long())   # Convert to int64
print("Half Tensor (float16):", tensor.half())   # Convert to float16
print("Float Tensor (float32):", tensor.float())   # Convert to float32
print("Double Tensor (float64):", tensor.double())   # Convert to float64

Converting Between NumPy Arrays and Tensors

PyTorch makes it easy to switch between NumPy arrays and tensors, allowing seamless integration with existing computing workflows.

# Create a NumPy array of zeros
np_array = np.zeros((5, 5))
print("NumPy Array:\n", np_array)

# Convert NumPy array to PyTorch tensor
tensor = torch.from_numpy(np_array)
print("Tensor from NumPy Array:\n", tensor)

# Convert tensor back to NumPy array
numpy_back = tensor.numpy()
print("Converted Back to NumPy Array:\n", numpy_back)

Tensor Mathematics and Comparison Operations

This section explores essential math operations with PyTorch tensors.

Addition & Subtraction: Adds and subtracts two tensors element-wise.
Division: Uses true division for precise results.
Inplace Operations: Modifies a tensor directly without creating a new one.
Exponentiation: Raises each element to a power using pow() or **.
Comparisons: Checks conditions like x > 0 or x < 0, returning boolean results.
Dot Product: Computes the sum of element-wise multiplications between two tensors.

# Define two tensors for operations
x = torch.tensor([1, 2, 3])
y = torch.tensor([9, 8, 7])

# Addition
z = x + y

# Addition using .add
z1 = torch.empty(3)
torch.add(x, y, out=z1)
z2 = torch.add(x, y)
print("Addition Results:", z, z1, z2)

# Subtraction
z = x - y
print("Subtraction Result:", z)

# Division (true division)
z = torch.true_divide(x, y)
print("Division Result:", z)

# Inplace operations
t = torch.ones(3)
print("Before inplace addition:", t)
t.add_(x)
print("After inplace addition:", t)
t += x  # Another inplace addition (note: t = t + x creates a new tensor)
print("After second inplace addition:", t)

# Exponentiation
z = x.pow(2)
print("Exponentiation (pow):", z)
z = x**2
print("Exponentiation (**):", z)

# Comparisons
z = x > 0
print("x > 0:", z)
z = x < 0
print("x < 0:", z)

# Dot product
z = torch.dot(x, y)
print("Dot Product:", z)

Matrix Multiplication and Batch Operations

Matrix operations are at the heart of deep learning. Let's find out different ways to perform multiplication.

Matrix Multiplication: Uses @ or torch.mm() to perform standard matrix multiplication.
Matrix Exponentiation: Raises a square matrix to a power using matrix_power(n).
Element-wise Multiplication: Uses torch.mul() or * for element-wise multiplication.
Batch Matrix Multiplication: Uses torch.bmm() to multiply batches of matrices efficiently.

# Matrix multiplication using @ operator and torch.mm
x2 = torch.tensor([[1, 2, 3]])
y2 = torch.tensor([[9, 8, 7]])

z = x2 @ torch.t(y2)
print("Matrix Multiplication (@ operator):\n", z)

z = torch.mm(x2, torch.t(y2))
print("Matrix Multiplication (torch.mm):\n", z)

z = x2.mm(torch.t(y2))
print("Matrix Multiplication (mm):\n", z)

# Matrix exponentiation: multiplying a matrix with itself 3 times
matrix_exp = torch.rand(5, 5)
print("Matrix multiplied 3 times:\n", matrix_exp @ matrix_exp @ matrix_exp)
print("Matrix power 3:\n", matrix_exp.matrix_power(3))

# Element-wise multiplication
z = torch.mul(x, y)
print("Element-wise Multiplication:", z)
z = x * y
print("Element-wise Multiplication (alternative):", z)

# Batch matrix multiplication
batch = 32
n = 10
m = 20
p = 30

tensor1 = torch.rand((batch, n, m))
tensor2 = torch.rand((batch, m, p))

out_bmm = torch.bmm(tensor1, tensor2)  # Result shape: (batch, n, p)
print("Batch Matrix Multiplication (first batch):\n", out_bmm[0])
print("Shape of batched multiplication result:", (tensor1 @ tensor2).shape)

Broadcasting and Other Useful Operations

Broadcasting allows arithmetic operations on tensors of different shapes. This section also demonstrates additional useful functions.

Broadcasting: Automatically expands smaller tensors to match larger ones in operations.
Summation: torch.sum(x, dim=0) computes sum along a specific dimension.
Min/Max Values: torch.max() and torch.min() return the highest and lowest values along a dimension.
Absolute Values: torch.abs(x) gets the element-wise absolute values.
Argmax/Argmin: torch.argmax() and torch.argmin() return the index of max/min values.
Mean Calculation: torch.mean(x.float(), dim=0) computes the mean (ensuring float dtype).
Element-wise Comparison: torch.eq(x, y) checks equality between two tensors.
Sorting: torch.sort(y, dim=0) sorts tensor elements and returns indices.
Clamping: torch.clamp(x, min=0) restricts values within a range.
Boolean Operations: torch.any(x_bool) checks if any value is True, torch.all(x_bool) checks if all are True.

# Broadcasting example
x1 = torch.rand(5, 5)
x2 = torch.rand(5)
print("Tensor x1:\n", x1)
print("Tensor x2:\n", x2)
print("x1 - x2:\n", x1 - x2)
print("x1 raised to the power of x2:\n", x1 ** x2)

# Sum of tensor elements along dimension 0
sum_x = torch.sum(x, dim=0)
print("Sum along dimension 0:", sum_x)

# Maximum and minimum values
value, indices = torch.max(x, dim=0)
print("Max value and index:", value, indices)

value, indices = torch.min(x, dim=0)
print("Min value and index:", value, indices)

# Other operations
print("Absolute values:", torch.abs(x))
print("Argmax:", torch.argmax(x, dim=0))
print("Argmin:", torch.argmin(x, dim=0))
print("Mean (converted to float):", torch.mean(x.float(), dim=0))
print("Element-wise equality (x == y):", torch.eq(x, y))

# Sorting
sorted_y, indices = torch.sort(y, dim=0, descending=False)
print("Sorted y and indices:", sorted_y, indices)

# Clamping values
print("Clamped x:", torch.clamp(x, min=0))

# Boolean operations
x_bool = torch.tensor([1, 0, 1, 1, 1], dtype=torch.bool)
print("Any True:", torch.any(x_bool))
print("All True:", torch.all(x_bool))

Tensor Indexing

Access and modify tensor elements using indexing, slicing, and advanced indexing.

Accessing Rows & Columns: Use x[row, :] for a row and x[:, col] for a column.
Slicing: x[row, start:end] extracts a portion of a row.
Modifying Elements: Directly assign values using x[row, col] = value.
Fancy Indexing: Use a list of indices to select multiple elements at once.
Conditional Indexing: Extract elements using conditions like (x < 2) | (x > 8).
Finding Even Numbers: Use x.remainder(2) == 0 to filter even values.
Conditional Selection with torch.where(): Chooses values based on a condition.

# Create a random tensor with shape (batch_size, features)
batch_size = 10
features = 25
x = torch.rand((batch_size, features))

# Access the first row
print("First row of tensor:", x[0, :])

# Access the second column
print("Second column of tensor:", x[:, 1])

# Access the first 10 elements of the third row
print("First 10 elements of third row:", x[2, 0:10])

# Modify a specific element (set first element to 100)
x[0, 0] = 100

# Fancy indexing example
x1 = torch.arange(10)
indices = [2, 5, 8]
print("Fancy indexing result:", x1[indices])

# Advanced indexing: select elements based on a condition
x2 = torch.arange(10)
print("Elements where x2 < 2 or x2 > 8:", x2[(x2 < 2) | (x2 > 8)])
print("Even numbers in x2:", x2[x2.remainder(2) == 0])

# Using torch.where to select values based on a condition
print("Using torch.where:", torch.where(x2 > 5, x2, x2 * 2))

Tensor Reshaping

Learn how to reshape tensors, concatenate them, and change the order of dimensions.

Reshape with view() & reshape(): Change tensor shape without altering data.
Transpose & Flatten: .t() transposes, .contiguous().view(-1) flattens.
Concatenation: torch.cat([x1, x2], dim=0/1) merges tensors along rows/columns.
Flattening: .view(-1) converts tensor into a 1D array.
Batch Reshaping: .view(batch, -1) keeps batch size while reshaping.
Permute Dimensions: .permute(0, 2, 1) reorders dimensions efficiently.
Unsqueeze for New Dimensions: .unsqueeze(dim) adds singleton dimensions.

# Reshape a tensor using view and reshape
x = torch.arange(9)
x_3x3 = x.view(3, 3)
print("Reshaped to 3x3 using view:\n", x_3x3)
x_3x3 = x.reshape(3, 3)
print("Reshaped to 3x3 using reshape:\n", x_3x3)

# Transpose and flatten the tensor
y = x_3x3.t()
print("Flattened transposed tensor:", y.contiguous().view(9))

# Concatenation example
x1 = torch.rand(2, 5)
x2 = torch.rand(2, 5)
print("Concatenated along dimension 0 (rows):", torch.cat([x1, x2], dim=0).shape)
print("Concatenated along dimension 1 (columns):", torch.cat([x1, x2], dim=1).shape)

# Flatten the tensor using view(-1)
z = x1.view(-1)
print("Flattened tensor shape:", z.shape)

# Reshape with batch dimension
batch = 64
x = torch.rand(batch, 2, 5)
print("Reshaped to (batch, -1):", x.view(batch, -1).shape)

# Permute dimensions
z = x.permute(0, 2, 1)
print("Permuted tensor shape:", z.shape)

# Unsqueeze examples (adding new dimensions)
x = torch.arange(10)
print("Original x:", x)
print("x unsqueezed at dim 0:", x.unsqueeze(0).shape, x.unsqueeze(0))
print("x unsqueezed at dim 1:", x.unsqueeze(1).shape, x.unsqueeze(1))

👉 Code: https://github.com/analyticalrohit/pytorch_fundamentals

🚀 Clone the repository and start exploring!

Liked this article? Make sure to 💜 click the like button.

Feedback or addition? Make sure to 💬 comment.

Know someone that would find this helpful? Make sure to 🔁 share this post.

Get in touch

You can find me on LinkedIn | YouTube | GitHub | X

Book an Appointment: Topmate

If you wish to make a request on particular topic you would like to read, you can send me an email to analyticalrohit.connect@gmail.com